动态规划 算法专辑之子数组问题（1）

本专栏将从状态定义、状态转移方程、初始化、填表顺序、返回值这五大细节来详细讲述动态规划的算法的解题思路及代码实现

一、什么是子数组

子数组：子数组是数组中的一个连续部分的集合，子序列可以不连续，但子数组的元素必定在原数组中是连续的

二、leetcode.cn/problems/maximum-subarray/">最大子数组和

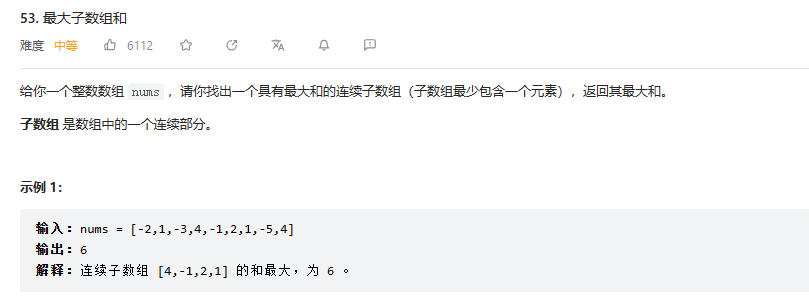
1.题目解析

在n个子数组中，找到和最大的那个，并返回该子数组元素的总和

2.状态定义

根据经验+题目要求，dp[i]表示：以i下标为结尾的子数组中最大的和

3.状态转移方程

这题和最长递增子序列分析相似，dp[i]同样分为长度为1和长度大于1这两种情况

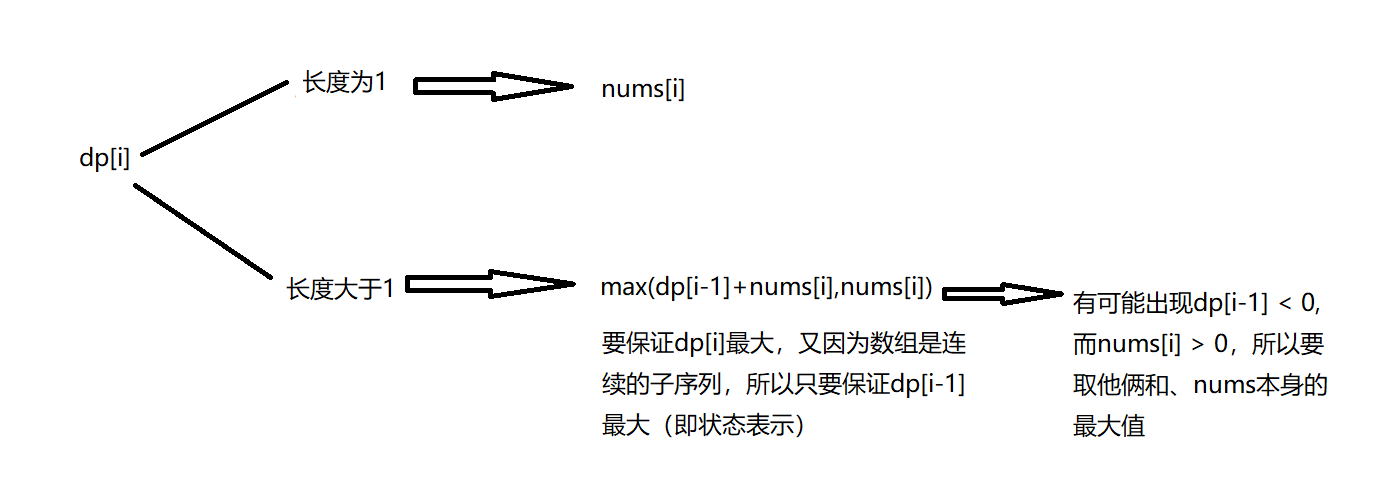
由上诉分析可得如下的状态转移方程：

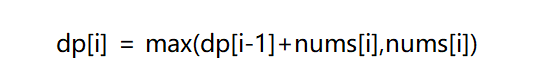
4.初始化

在之前的子序列问题中，我们是按照长度为1的情况下来对dp表进行初始化，但这题将整个dp表初始化的话，反而冗余了，只需初始化dp[0]即可（在子序列问题中，是和dp表进行比较，此题是和nums进行比较）

5.填表顺序

可以看到在dp表中，i收到i-1的影响，所以应该从左到右进行填表

6.返回值

这和之前的子序列问题也类似，返回的应该是dp表中的最大值

7.代码实现

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n);
        dp[0] = nums[0];
        int res = nums[0];
        for(int i=1;i<n;i++)
        {
            dp[i] = max(dp[i-1] + nums[i],nums[i]);
            res = max(res,dp[i]);
        }

        return res;
    }
};

三、leetcode.cn/problems/maximum-sum-circular-subarray/">环形子数组的最大和

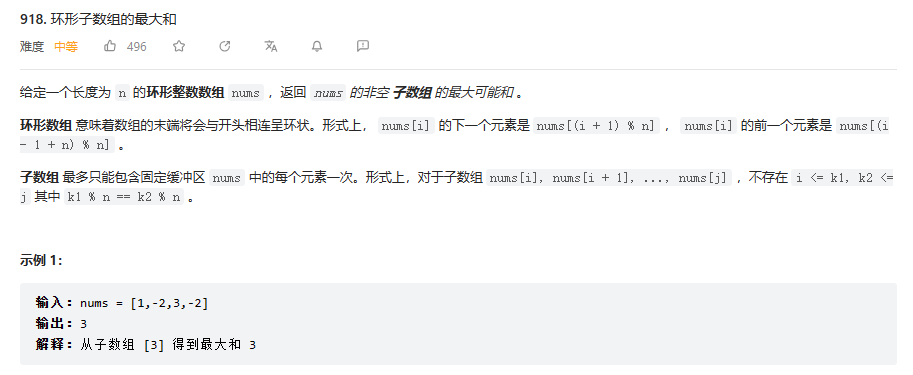
1.题目解析

本题是上面那题的变形题，将线性的数组，变为了环形，也就是说首尾可以相连，在原题上上升了一定难度

2.状态定义

根据经验+题目要求，dp[i]表示：以下标i结尾的所有环形子数组的和的最大值

状态分析：

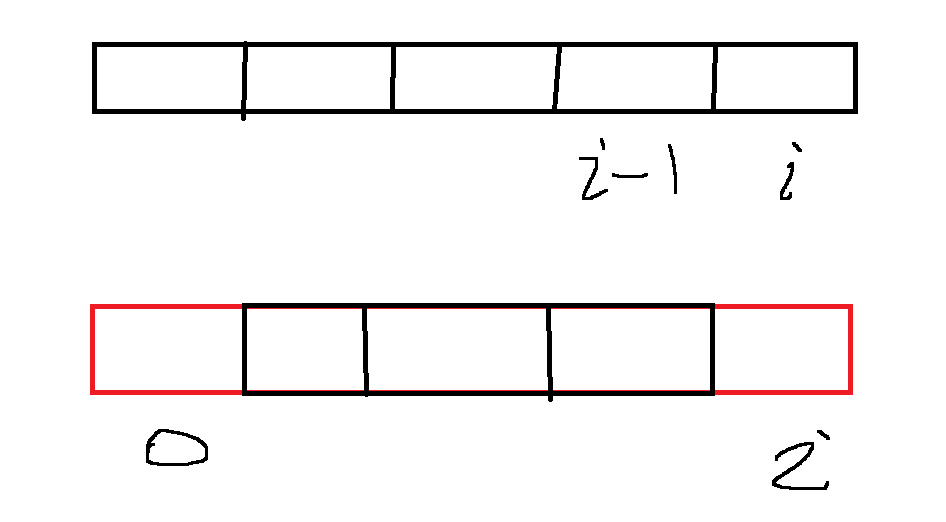
由上图我们可以看到，原来的状态定义只能满足下标是连续的状态，对于第二种情况处理起来十分麻烦，在数学上有一种思路：正难则反，既然算收尾相连是麻烦的，除去了首尾相连的子数组，剩下的子数组必然连续，那么就可以复用原来的状态转移方程了，要保证首尾相连最大，数组总和是确定的，所以只需保证剩余子数组和最小

由上述分析，此题因有两个不同且相互独立的子问题，因此要定义两种不同的状态：

f[i]表示：以下标i结尾的所有环形子数组的和的最大值

g[i]表示：以下标i结尾的所有环形子数组的和的最小值

3.状态转移方程

经过上述的分析，状态转移方程也应该有两个：

4.初始化

和上题一样，初始化dp[0]就行

5.填表顺序

经过上述的变形，使得两个dp表中i都只受i-1影响，因此可以从左到右进行填表

试想，如果直接计算首尾相连的情况，还能直接从左到右填表吗？

6.返回值

能直接返回max(fmax,sum - gmin)吗（fmax是f表里的最大值，gmin同理）

很显然是不能的，当数组里的所有元素都为负数时，返回的会是0，全是负数的子数组的和可能出现0吗？

因此，当全负数时，因返回fmax

为了减少单独计算数组总和这一步骤，我们只需在更新dp表的同时计算总和，在最后判断sum和gmin是否相等（详情见代码）

7.代码实现

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n+1,0);
        auto g = f;
        int fmax = INT_MIN;
        int gmin = INT_MAX;
        int sum = 0;
        for(int i=1;i<n+1;i++)
        {
            int x = nums[i-1];
            f[i] = max(x,f[i-1]+x);
            fmax = max(fmax,f[i]);
            g[i] = min(x,g[i-1]+x);
            gmin = min(gmin,g[i]);
            sum += x;
        }
        

        return sum == gmin ? fmax : max(fmax,sum - gmin);
    }
};